Rethinking tipping points in spatial ecosystems
Swarnendu Banerjee, Mara Baudena, Paul Carter, Robbin Bastiaansen, Arjen
Doelman, Max Rietkerk (2025)
[DOI]
American Naturalist
Abstract
Tipping point theory has garnered substantial attention over the last decades. It predicts abrupt and often irreversible transitions from one ecosystem state to an alternative state. However, typically, ecosystem models that predict tipping neglect spatial dynamics. Recent studies reveal that incorporating spatial dynamics may enable ecosystems to evade tipping predicted by nonspatial models. Here, we use a dryland and a savanna-forest model to synthesize mechanisms by which spatial processes can alter the theory of tipping. We further propose that the underlying drivers of positive feedback leading to alternative stable states may provide insight into the tipping evasion mechanisms most relevant to a specific ecosystem. For instance, while positive feedbacks may arise in drylands from direct self-facilitation, such as enhancing the uptake of a limiting resource, at the savanna-forest boundary, it may arise from mutual inhibition between two ecosystem components. In the former case, ecosystems can evade tipping by forming self-organized patterns, whereas in the latter, the presence of environmental heterogeneity may be required. Our study highlights that deepening our understanding of how ecological feedbacks connect to tipping evasion mechanisms is crucial to formulate better strategies to increase ecosystem resilience.
Early warning skill, extrapolation and tipping for accelerating cascades
Peter Ashwin, Robbin Bastiaansen , Anna von der Heydt, Paul Ritchie (2025)
[DOI]
Proc. R. Soc. A.48120250405
Abstract
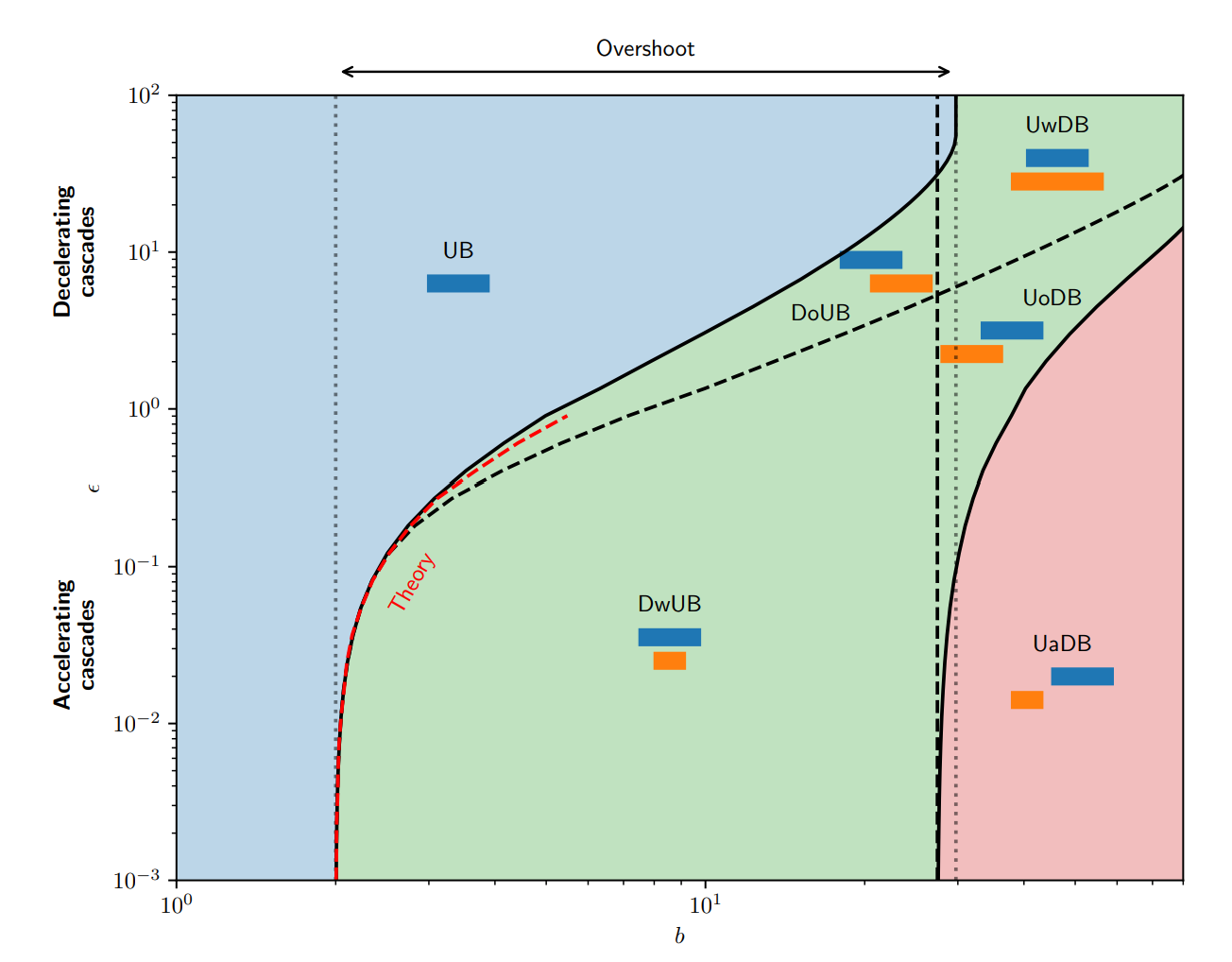
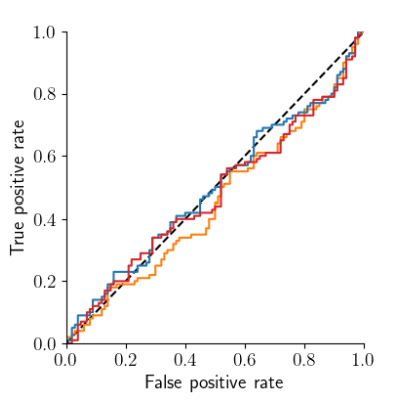
We investigate how nonlinear behaviour (both of forcing in time and of the system itself) can affect the skill of early warning signals to predict tipping in (directionally) coupled bistable systems when using measures based on critical slowing down due to the breakdown of extrapolation. We quantify the skill of early warnings with a time horizon using a receiver-operator methodology for ensembles where noise realisations and parameters are varied to explore the role of extrapolation and how it can break down. We highlight cases where this can occur in an accelerating cascade of tipping elements, where very slow forcing of a slowly evolving ``upstream'' system forces a more rapidly evolving ``downstream'' system. If the upstream system crosses a tipping point, this can shorten the timescale of valid extrapolation. In particular, ``downstream-within-upstream'' tipping will typically have warnings only on a timescale comparable to the duration of the upstream tipping process, rather than the timescale of the original forcing.
Assessment of Abrupt Shifts in CMIP6 Models using Edge Detection
Sjoerd Terpstra, Swinda K.J. Falkena, Robbin Bastiaansen , Sebastian Bathiany, Henk A. Dijkstra, Anna S. von der Heydt (2025)
[DOI]
AGU Advances, 6, e2025AV001698
Abstract
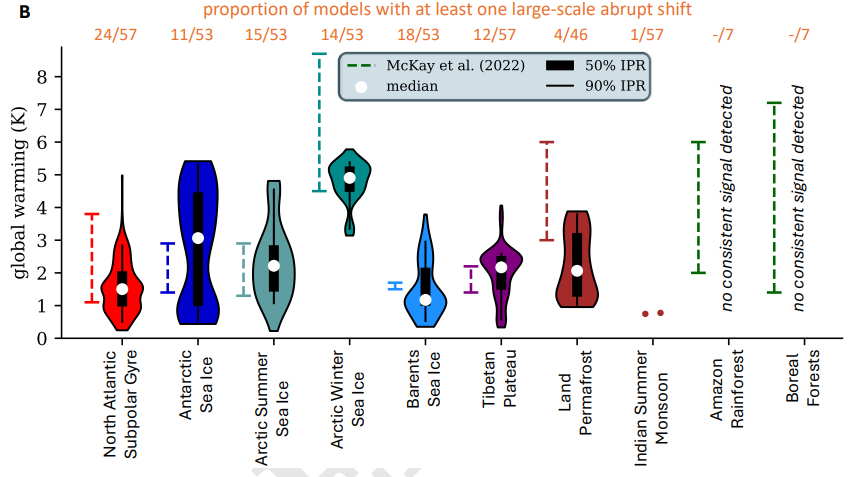
Research over the past decade has shown that multiple elements of the climate system, such as the Arctic Winter sea ice or the Amazon rainforest, could undergo abrupt shifts, but there are large uncertainties regarding their timing and spatial extent. In this study we investigated when and where abrupt shifts occur in the latest generation of climate models (CMIP6) under a scenario of a 1% annual increase in CO2. We considered 82 ocean, atmosphere, and land variables across 57 models. We used a Canny edge detection method -- adapted for spatiotemporal dimensions -- to detect abrupt shifts occurring on time scales from years to decades. Then, we performed a connected component analysis to quantify the spatial extent of these shifts. The systems analyzed include the North Atlantic subpolar gyre, Tibetan Plateau, land permafrost, Amazon rainforest, Antarctic sea ice, monsoon systems, Arctic summer sea ice, Arctic winter sea ice, and Barents sea ice. With the exception of the monsoons systems, we found abrupt shifts in multiple models per system. We observed a considerable variation across the different CMIP6 models in terms of timing and spatial extent. Higher levels of global warming increased the risk of abrupt shifts in CMIP6 models. Even at a global warming level of 1.5C, six out of ten studied climate subsystems showed abrupt shifts that cover a substantial area in multiple models.
Approximating the bifurcation diagram of weakly and strongly coupled leading-following systems
Sacha Sinet, Robbin Bastiaansen , Christian Kuhn, Anna S. von der Heydt, Henk. A. Dijkstra (2025)
Abstract
The potential of dynamical systems to undergo bifurcation-induced tipping has received much attention recently in climate and ecology research. In particular, such systems can form an intricate interacting network, creating the possibility of cascading critical transitions in which tipping of one element results in the tipping of another. In this paper, we focus on unidirectionally coupled scalar subsystems in which one component is driven by a polynomial equation. We investigate such interacting systems beyond the so-far used setting of linearly interacting bistable subsystems. In these cases, we show how the bifurcation diagram of the coupled system can be approximated using asymptotic methods, starting from the simpler bifurcation diagram of the decoupled problems. We study the limits in which the coupling is weak or strong, yielding approximations of the equilibrium branches and their stability. Those results are illustrated using conceptual models for the ocean circulation driven by wind and density and for the interacting ocean circulation and Amazon rainforest.

Evaluating Empirical Dynamic Modeling for forecasting: The role of variation among time series replicates
Fleur Slegers, Robbin Bastiaansen, Edwin Pos (2025)
[DOI]
Ecological Informatics
Abstract
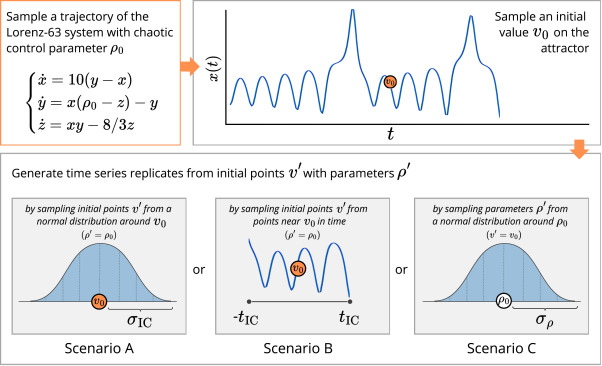
Accurate forecasting of ecological systems is essential for effective environmental management but remains challenging. One tool for this purpose is Empirical Dynamic Modeling (EDM). EDM typically requires long time series as input. To overcome data limitations, time series from similar sources (replicates) are often combined. Although EDM with replicates has been evaluated using simulated data, the impact of adding time series remains not fully understood. In this study, we use simulated data from the Lorenz-63 system, a three-species food chain, and a four-species Lotka–Volterra model of competition to evaluate the performance of EDM’s S-Map algorithm across various scenarios, employing three different approaches to generate time series replicates, each with a different type of variation between the replicates: varying initial conditions (Scenario A), sampling distinct sections of the attractor (Scenario B), and varying the system’s parameter controlling chaotic behavior (Scenario C). Our findings demonstrate that EDM performs better with longer time series, but that combining replicates can often compensate for short time series length, in line with expectations from previous results. However, both the type and level of variation among the combined replicates affect forecasting accuracy. Adding replicates in Scenario B consistently improves outcomes. However, in Scenarios A and C (involving different long-term behaviors or transient phases), combining replicates may negate these benefits, particularly for periodic and chaotic systems and large inter-replicate variations. Our results show that not all time series replicates are equally suitable for improving EDM forecasts, highlighting the importance of careful selection and combination of replicates.
Ecosystem Resilience Monitoring and Early Warning Using Earth Observation Data: Challenges and Outlook
Sebastian Bathiany, Robbin Bastiaansen, Ana Bastos, Lana Blaschke, Jelle Lever, Sina Loriani, Wanda de Keersmaecker, Wouter Dorigo, Milutin Milenković, Cornelius Senf, Taylor Smith, Jan Verbesselt and Niklas Boers (2024)
[DOI]
Surveys in Geophysics
Abstract
As the Earth system is exposed to large anthropogenic interferences, it becomes ever more important to assess the resilience of natural systems, i.e., their ability to recover from natural and human-induced perturbations. Several, often related, measures of resilience have been proposed and applied to modeled and observed data, often by different scientific communities. Focusing on terrestrial ecosystems as a key component of the Earth system, we review methods that can detect large perturbations (temporary excursions from a reference state as well as abrupt shifts to a new reference state) in spatio-temporal datasets, estimate the recovery rate after such perturbations, or assess resilience changes indirectly from stationary time series via indicators of critical slowing down. We present here a sequence of ideal methodological steps in the field of resilience science, and argue how to obtain a consistent and multi-faceted view on ecosystem or climate resilience from Earth observation (EO) data. While EO data offers unique potential to study ecosystem resilience globally at high spatial and temporal scale, we emphasize some important limitations, which are associated with the theoretical assumptions behind diagnostic methods and with the measurement process and pre-processing steps of EO data. The latter class of limitations include gaps in time series, the disparity of scales, and issues arising from aggregating time series from multiple sensors. Based on this assessment, we formulate specific recommendations to the EO community in order to improve the observational basis for ecosystem resilience research.
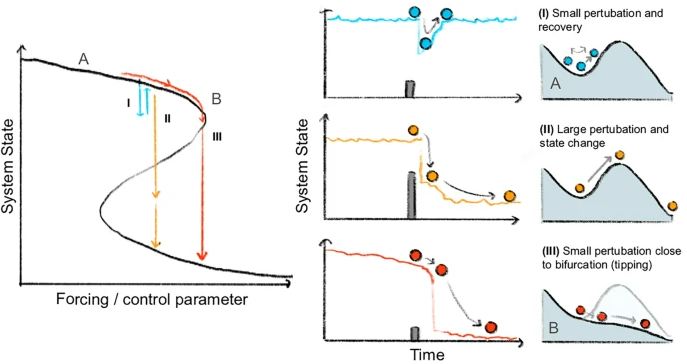
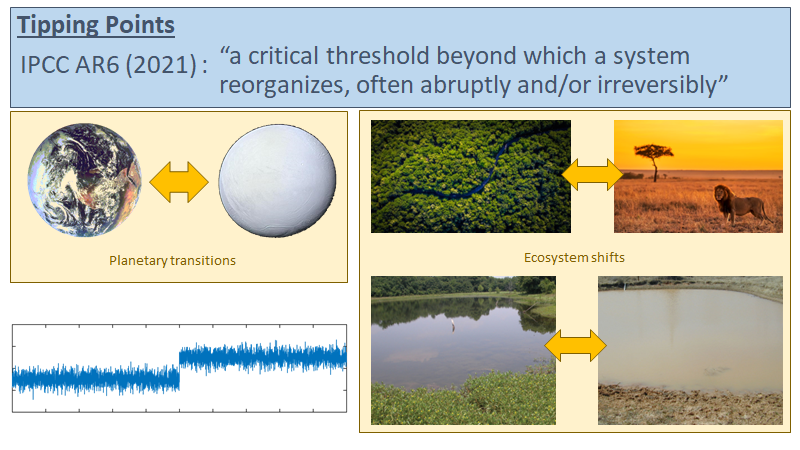
Climate tipping point interactions and cascades: A review
Nico Wunderling, Anna von der Heydt, Yevgeny Aksenov, Stephen Barker, Robbin Bastiaansen, Victor Brovkin, Maura Brunetti, Victor Couplet, Thomas Kleinen, Caroline H. Lear, Johannes Lohmann, Rosa Maria Roman-Cuesta, Sacha Sinet, Didier Swingedouw, Ricarda Winkelmann, Pallavi Anand, Jonathan Barichivich, Sebastian Bathiany, Mara Baudena, John T. Bruun, Christiano M. Chiessi, Helen K. Coxall, David Docquier, Jonathan F. Donges, Swinda K. J. Falkena, Ann Kristin Klose, David Obura, Juan Rocha, Stefanie Rynders, Norman Julius Steinert, and Matteo Willeit (2023)
[DOI]
Earth System Dynamics, 15, 41-74
Abstract
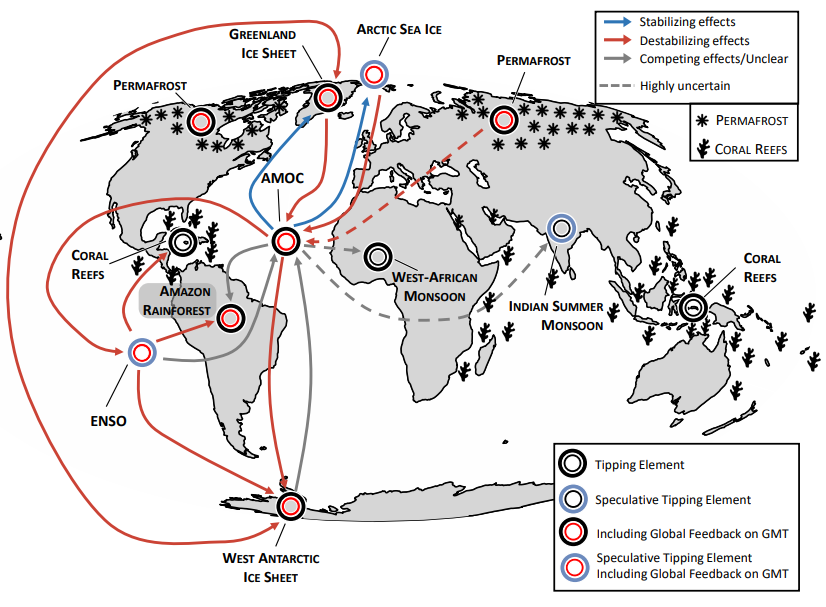
Climate tipping elements are large-scale subsystems of the Earth that may transgress critical thresholds (tipping points) under ongoing global warming, with substantial impacts on the biosphere and human societies. Frequently studied examples of such tipping elements include the Greenland Ice Sheet, the Atlantic Meridional Overturning Circulation (AMOC), permafrost, monsoon systems, and the Amazon rainforest. While recent scientific efforts have improved our knowledge about individual tipping elements, the interactions between them are less well understood. Also, the potential of individual tipping events to induce additional tipping elsewhere or stabilize other tipping elements is largely unknown. Here, we map out the current state of the literature on the interactions between climate tipping elements and review the influences between them. To do so, we gathered evidence from model simulations, observations, and conceptual understanding, as well as examples of paleoclimate reconstructions where multi-component or spatially propagating transitions were potentially at play. While uncertainties are large, we find indications that many of the interactions between tipping elements are destabilizing. Therefore, we conclude that tipping elements should not only be studied in isolation, but also more emphasis has to be put on potential interactions. This means that tipping cascades cannot be ruled out on centennial to millennial timescales at global warming levels between 1.5 and 2.0 ∘C or on shorter timescales if global warming surpassed 2.0 ∘C. At these higher levels of global warming, tipping cascades may then include fast tipping elements such as the AMOC or the Amazon rainforest. To address crucial knowledge gaps in tipping element interactions, we propose four strategies combining observation-based approaches, Earth system modeling expertise, computational advances, and expert knowledge.
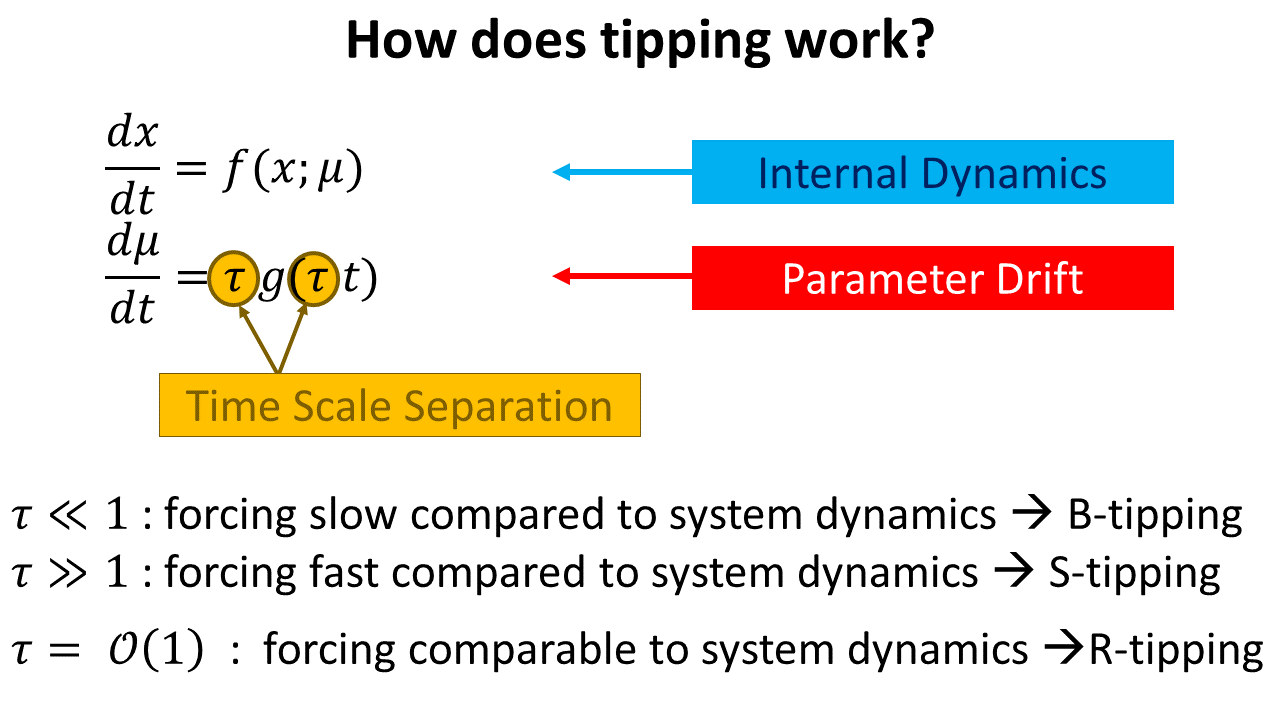
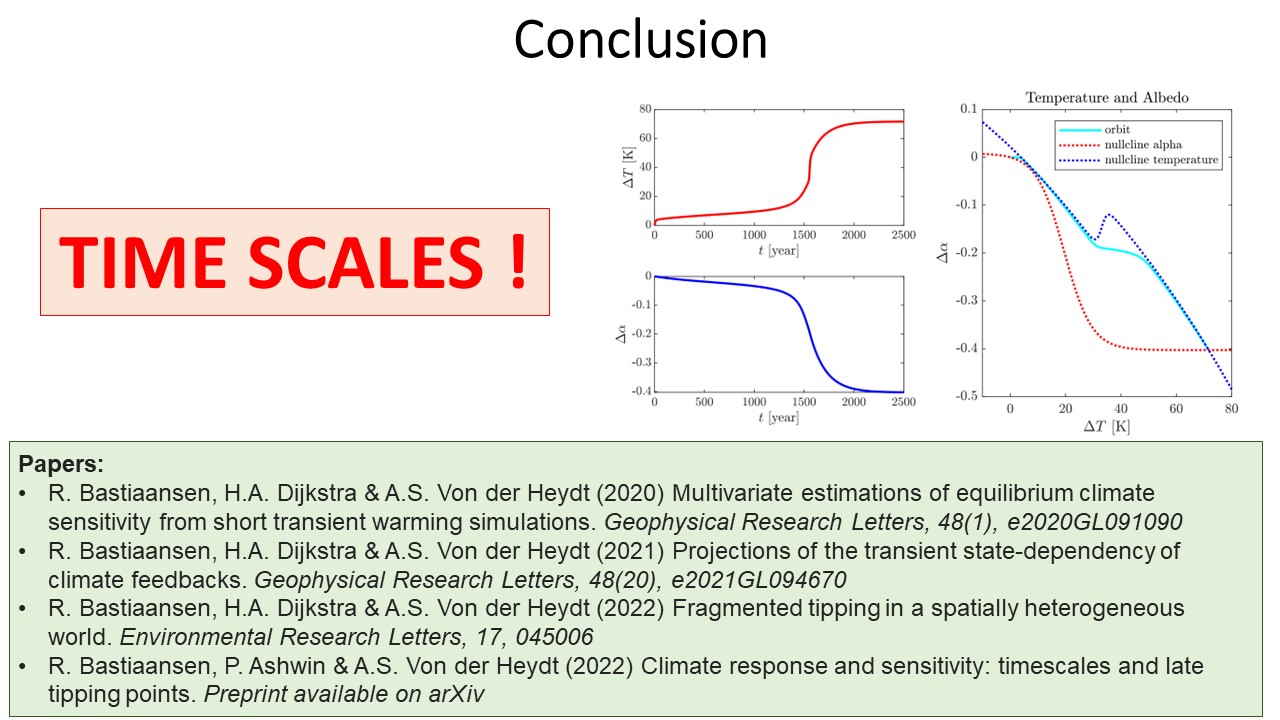
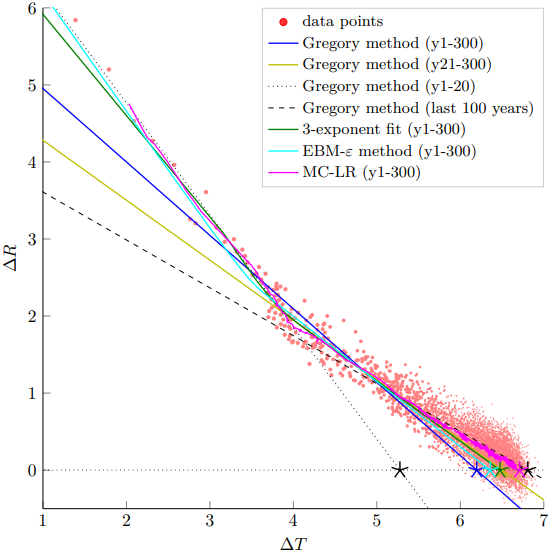
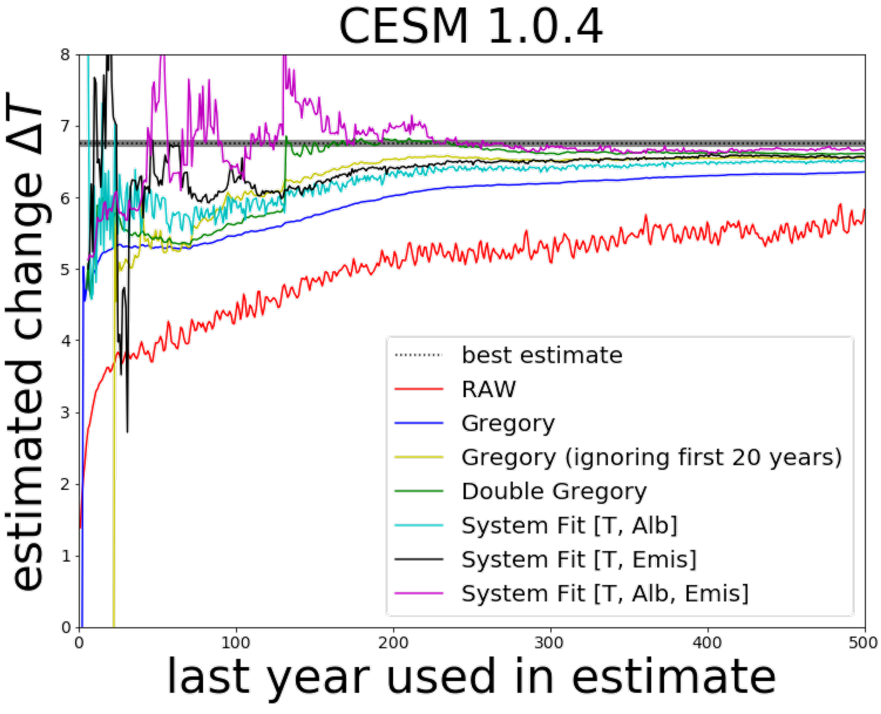
Climate Response and Sensitivity: Timescales and Late Tipping Points
Robbin Bastiaansen, Peter Ashwin, Anna S. von der Heydt (2023)
[DOI]
Proc. R. Soc. A.47920220483
Abstract
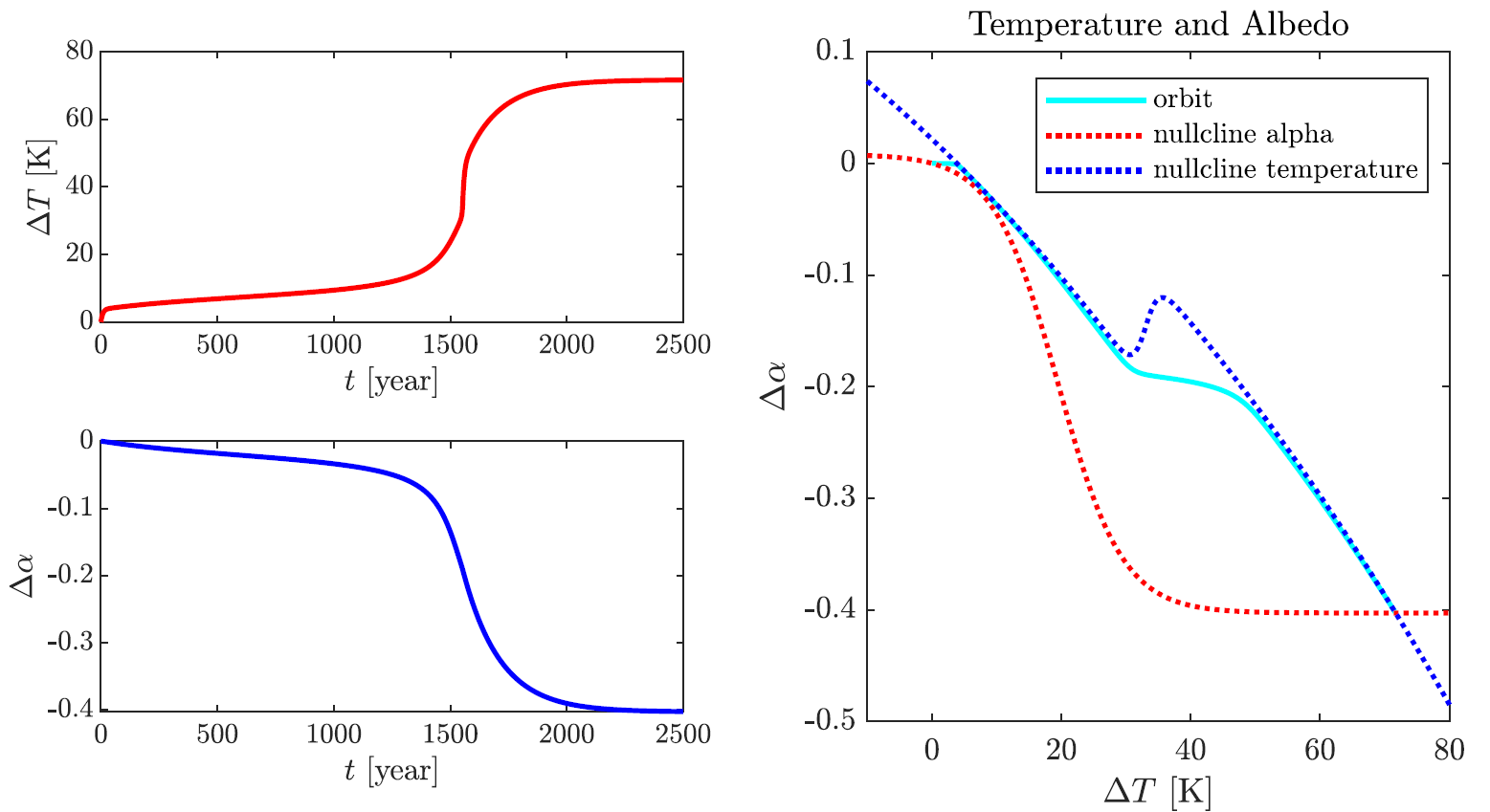
Climate response metrics are used to quantify the Earth's climate response to anthropogenic changes of atmospheric \COO. Equilibrium Climate Sensitivity (ECS) is one such metric that measures the equilibrium response to \COO\ doubling. However, both in their estimation and their usage, such metrics make assumptions on the linearity of climate response, although it is known that, especially for larger forcing levels, response can be nonlinear. Such nonlinear responses may become visible immediately in response to a larger perturbation, or may only become apparent after a long transient. In this paper, we illustrate some potential problems and caveats when estimating ECS from transient simulations. We highlight ways that very slow timescales may lead to poor estimation of ECS even if there is seemingly good fit to linear response over moderate timescales. Moreover, such slow timescale might lead to late abrupt responses ("late tipping points") associated with a system's nonlinearities. We illustrate these ideas using simulations on a global energy balance model with dynamic albedo. We also discuss the implications for estimating ECS for global climate models, highlighting that it is likely to remain difficult to make definitive statements about the simulation times needed to reach an equilibrium.
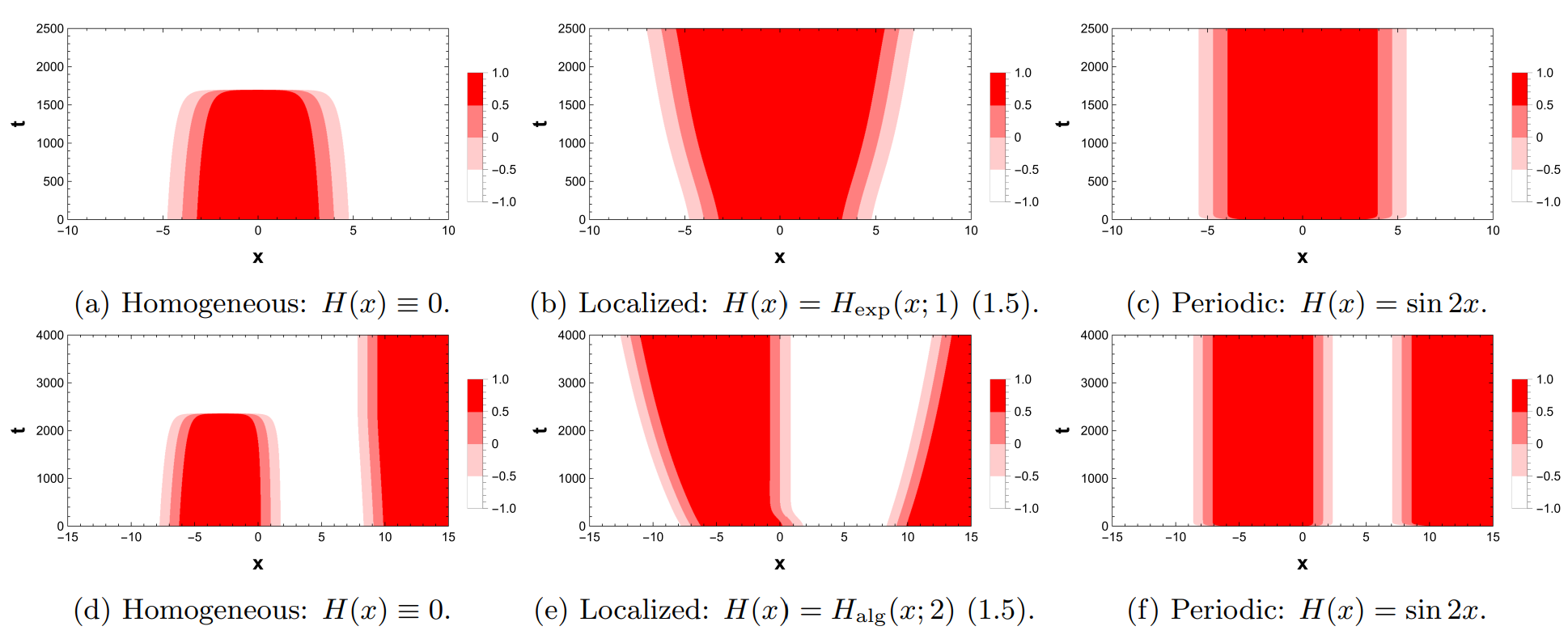
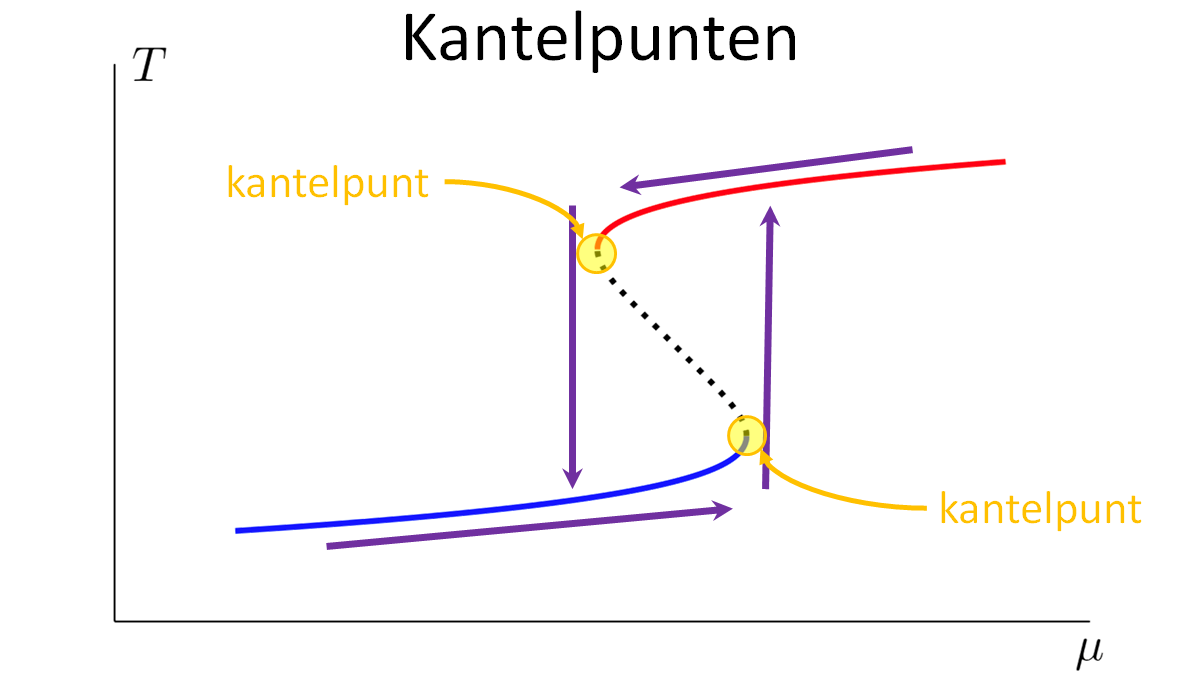
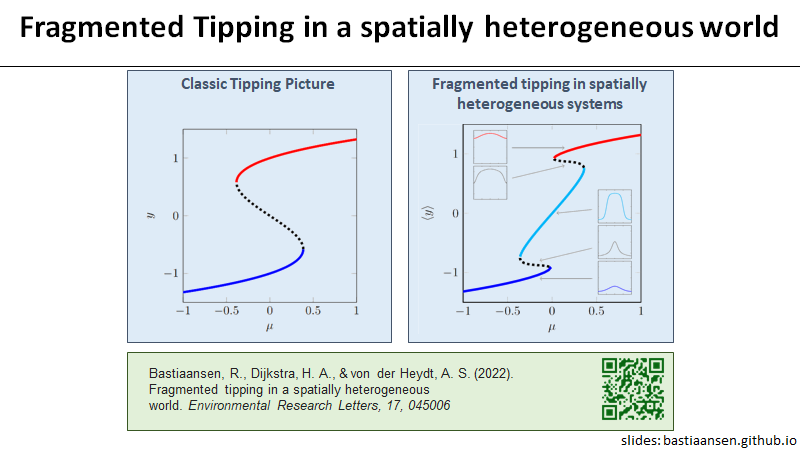
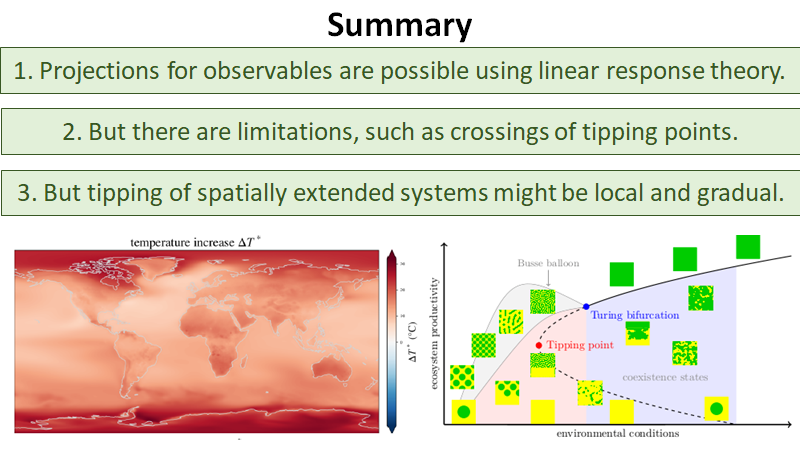
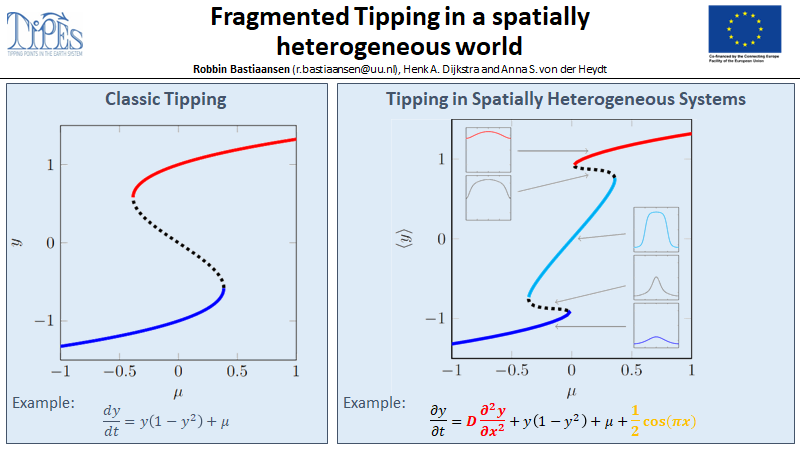
Fragmented tipping in a spatially heterogeneous world
Robbin Bastiaansen, Henk A. Dijkstra, Anna S. von der Heydt (2022)
[DOI]
Environmental Research Letters, 17, 045006
Abstract
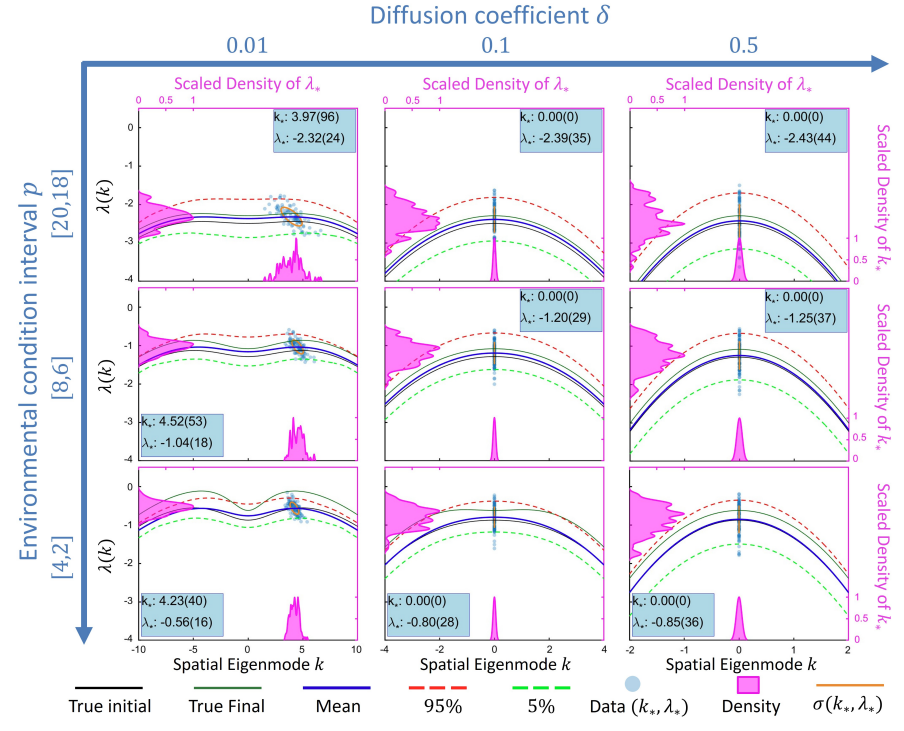
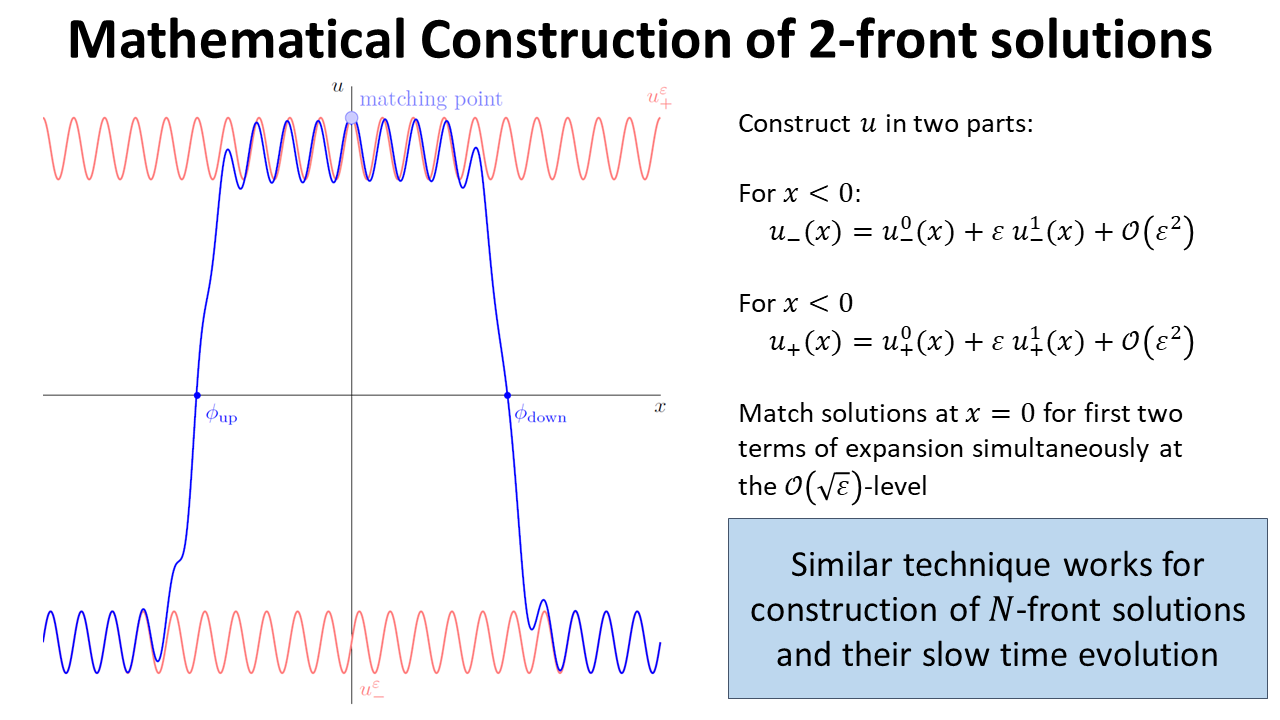
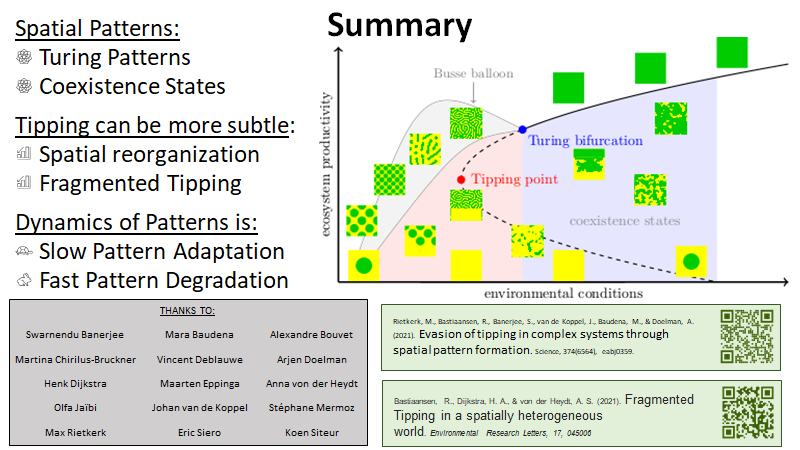
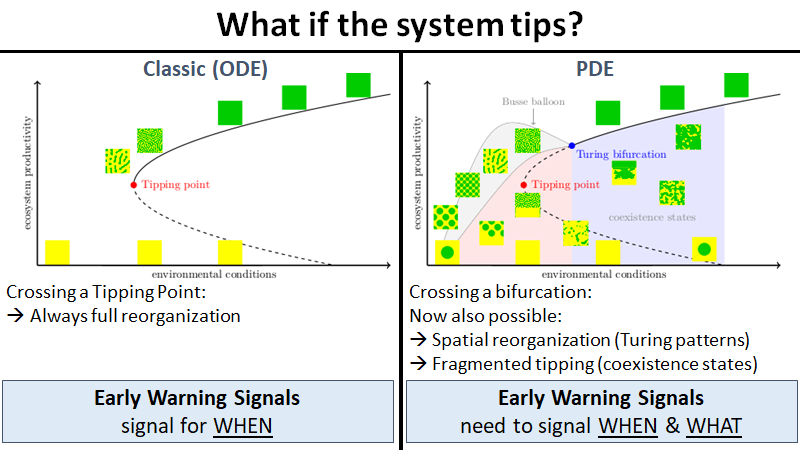
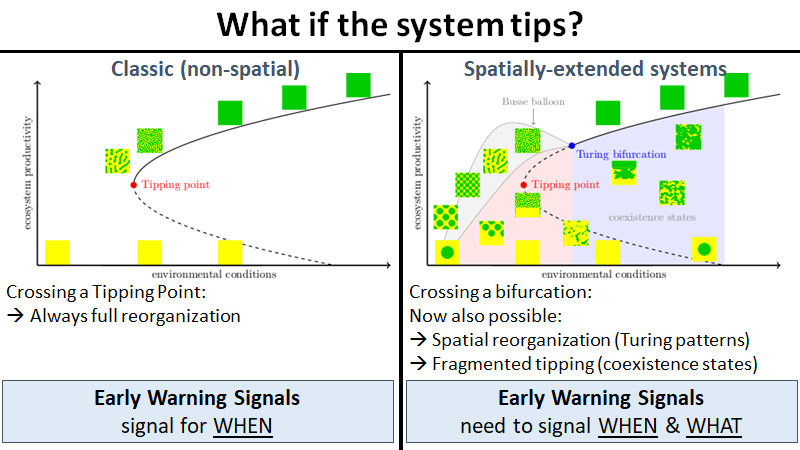
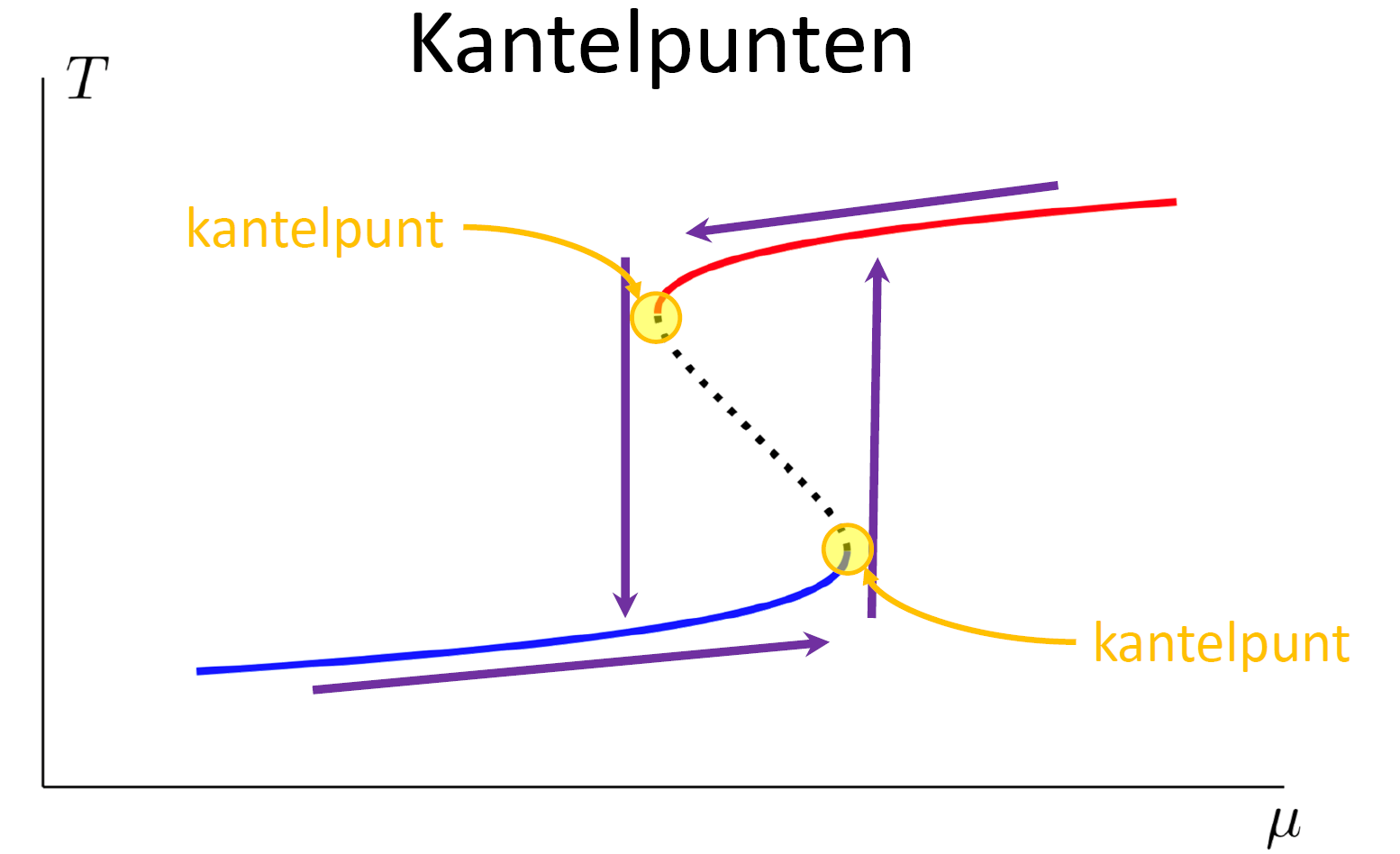
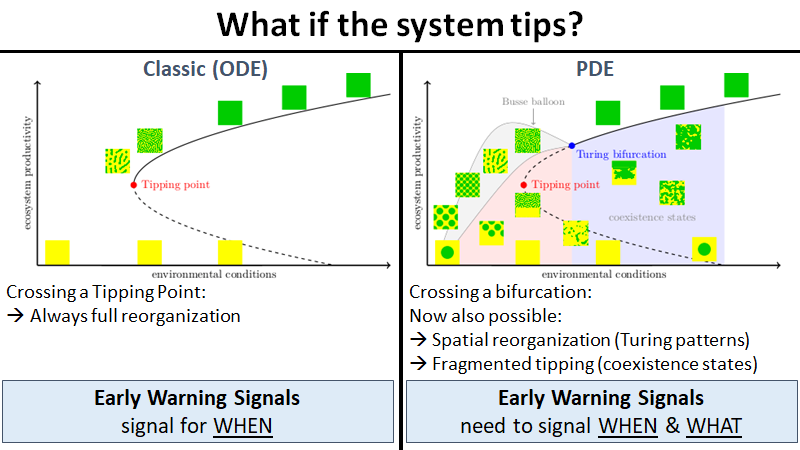
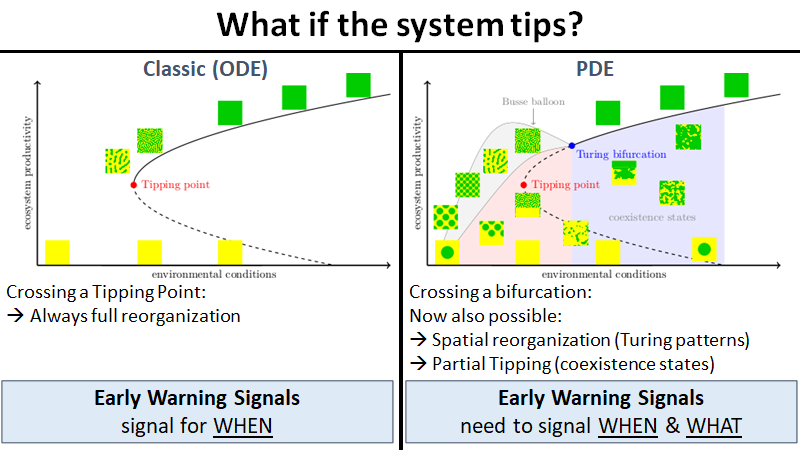
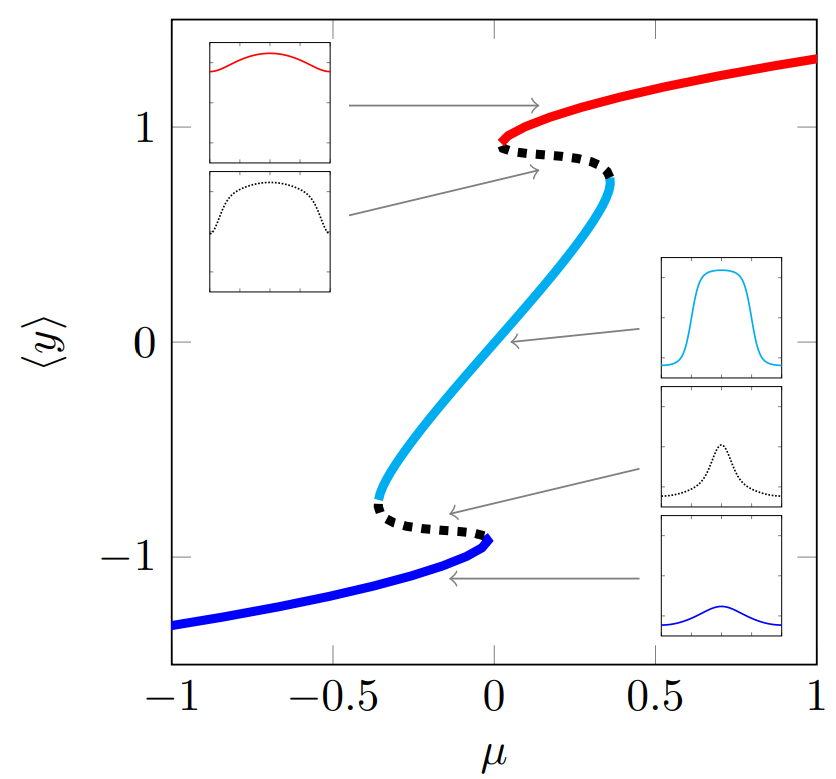
Many climate subsystems are thought to be susceptible to tipping—and some might be close to a tipping point. The general belief and intuition, based on simple conceptual models of tipping elements, is that tipping leads to reorganization of the full (sub)system. Here, we explore tipping in conceptual, but spatially extended and spatially heterogenous models. These are extensions of conceptual models taken from all sorts of climate system components on multiple spatial scales. By analysis of the bifurcation structure of such systems, special stable equilibrium states are revealed: coexistence states with part of the spatial domain in one state, and part in another, with a spatial interface between these regions. These coexistence states critically depend on the size and the spatial heterogeneity of the (sub)system. In particular, in these systems the crossing of a tipping point not necessarily leads to a full reorganization of the system. Instead, it might lead to a reorganization of only part of the spatial domain, limiting the impact of these events on the system's functioning.
Projections of the Transient State-Dependency of Climate Feedbacks
Robbin Bastiaansen, Henk A. Dijkstra, Anna S. von der Heydt (2021)
[DOI]
Geophysical Research Letters, 48(20), e2021GL094670
Abstract
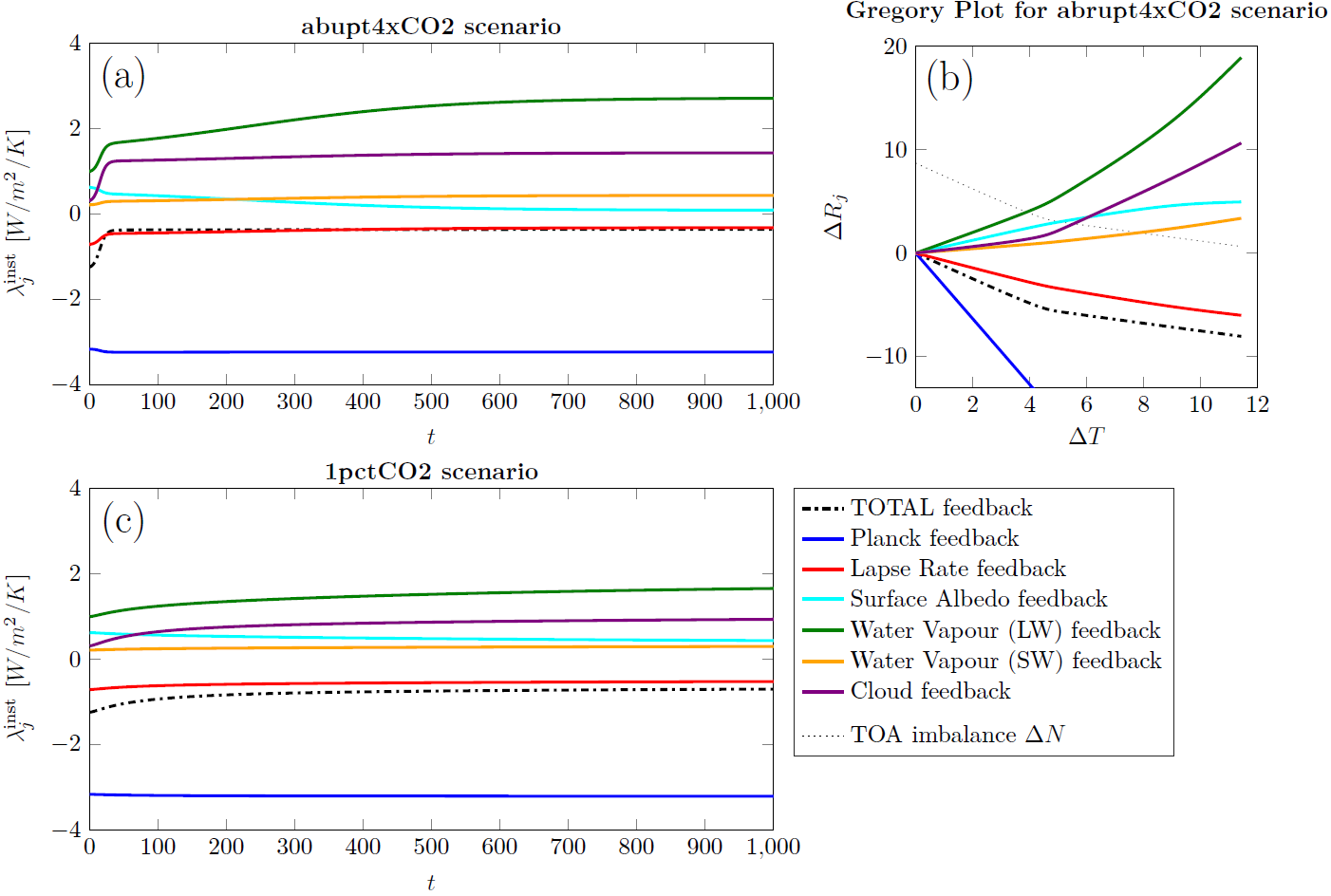
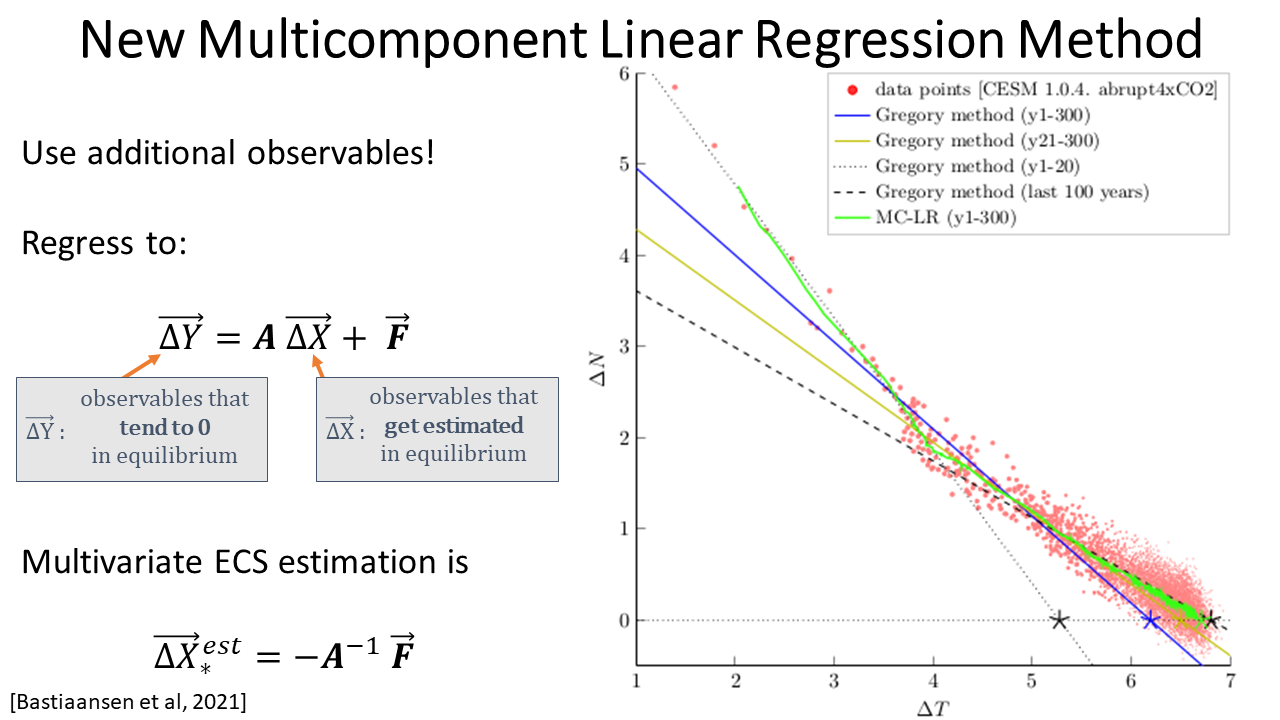
When the climate system is forced, e.g. by emission of greenhouse gases, it responds on multiple time scales. As temperatures rise, feedback processes might intensify or weaken. Such state dependencies cannot be fully captured with common linear regression techniques that relate feedback strengths linearly to changes in the global mean temperature. Hence, transient changes are difficult to track and it becomes easy to underestimate future warming this way. Here, we present a multivariate and spatial framework that facilitates dissection of climate feedbacks over time scales. Using this framework, information on the composition of projected transient future climates and feedback strengths can be obtained. The new framework is illustrated using the Community Earth System Model version 2 (CESM2).
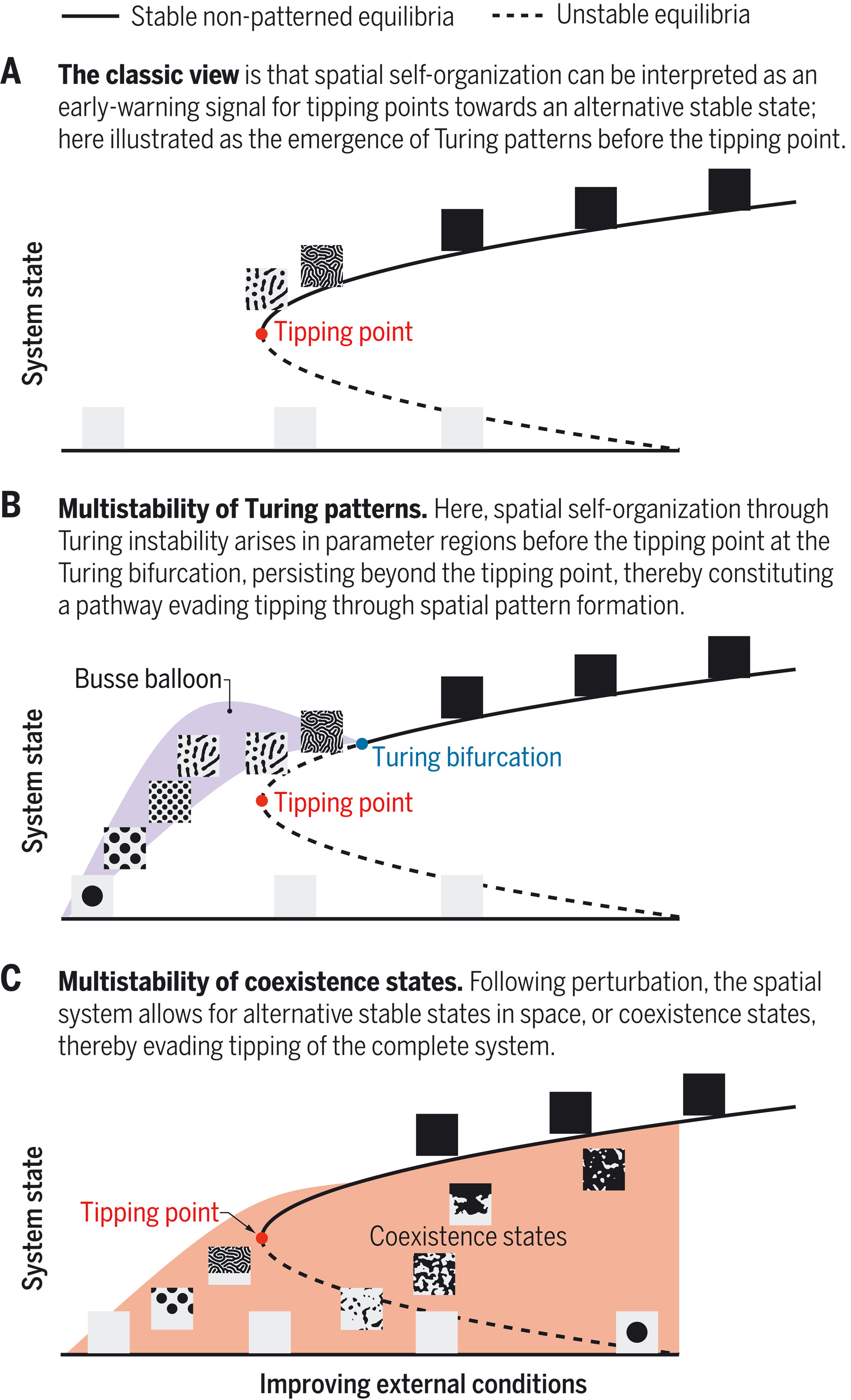
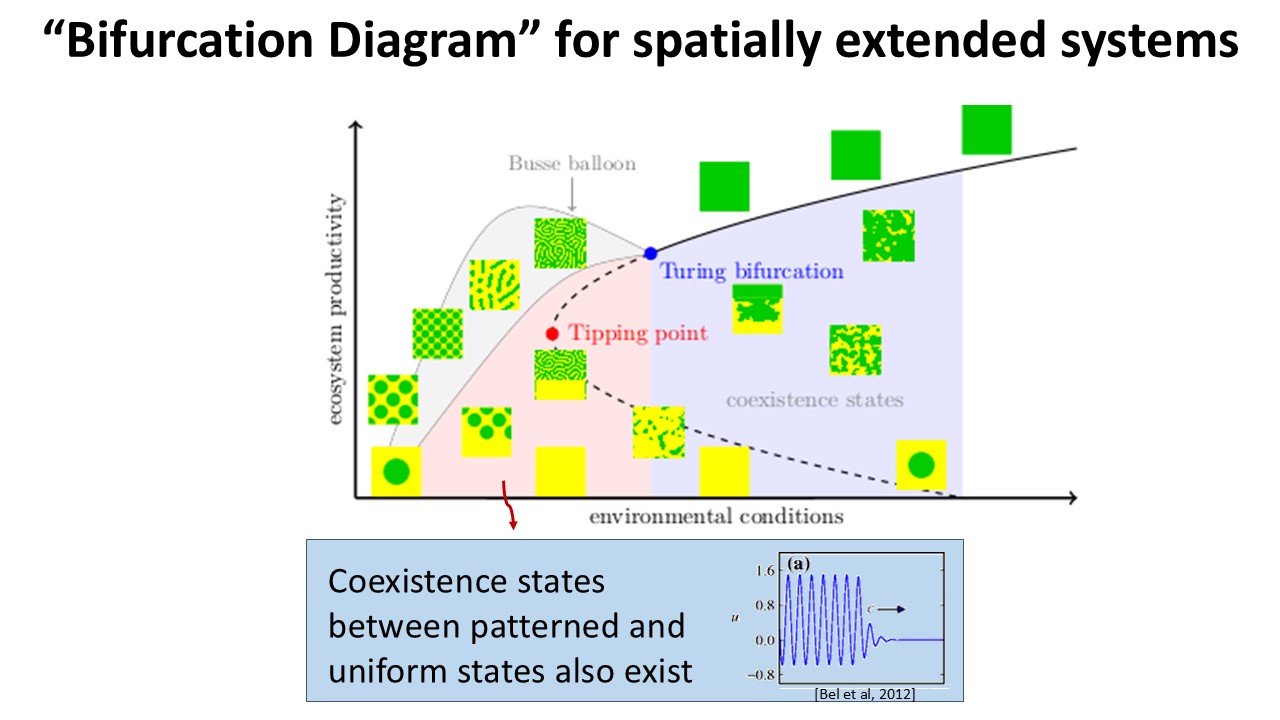
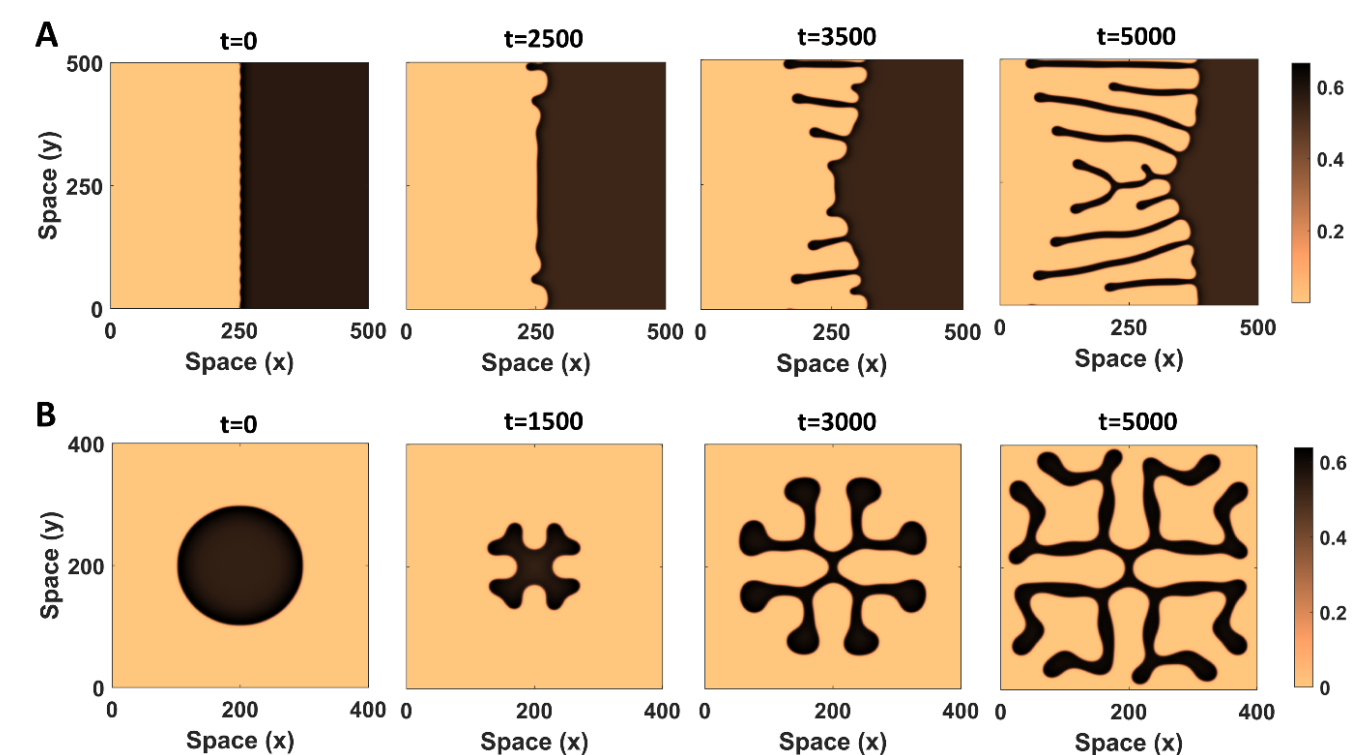
Evasion of tipping in complex systems through spatial pattern formation
Max Rietkerk, Robbin Bastiaansen, Swarnendu Banerjee, Johan van de Koppel, Mara Baudena, Arjen Doelman (2021)
[URL]
Science, 374(6564), eabj0359
Abstract
The concept of tipping points and critical transitions helps inform our understanding of the catastrophic effects that global change may have on ecosystems, Earth system components, and the whole Earth system. The search for early warning indicators is ongoing, and spatial self-organization has been interpreted as one such signal. Here, we review how spatial self-organization can aid complex systems to evade tipping points and can therefore be a signal of resilience instead. Evading tipping points through various pathways of spatial pattern formation may be relevant for many ecosystems and Earth system components that hitherto have been identified as tipping prone, including for the entire Earth system. We propose a systematic analysis that may reveal the broad range of conditions under which tipping is evaded and resilience emerges.
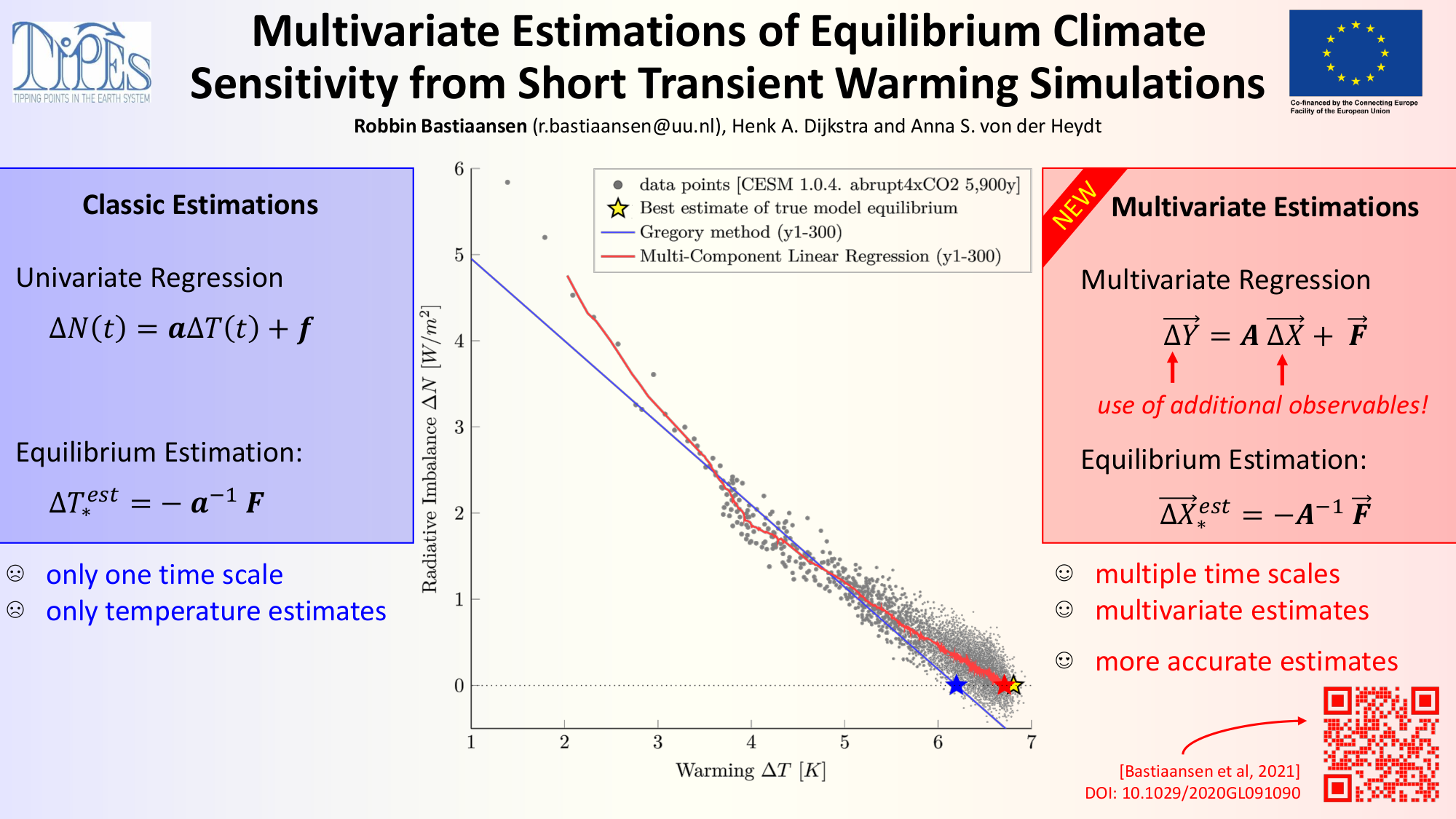
Multivariate estimations of equilibrium climate sensitivity from short transient warming simulations
Robbin Bastiaansen, Henk A. Dijkstra, Anna S. von der Heydt (2020)
[DOI]
Geophysical Research Letters, 48, e2020GL091090
Abstract
One of the most used metrics to gauge the effects of climate change is the equilibrium climate sensitivity, defined as the long-term (equilibrium) temperature increase resulting from instantaneous doubling of atmospheric CO2. Since global climate models cannot be fully equilibrated in practice, extrapolation techniques are used to estimate the equilibrium state from transient warming simulations. Because of the abundance of climate feedbacks - spanning a wide range of temporal scales - it is hard to extract long-term behaviour from short-time series; predominantly used techniques are only capable of detecting the single most dominant eigenmode, thus hampering their ability to give accurate long-term estimates. Here, we present an extension to those methods by incorporating data from multiple observables in a multi-component linear regression model. This way, not only the dominant but also the next-dominant eigenmodes of the climate system are captured, leading to better long-term estimates from short, non-equilibrated time series.
Modelling honey bee colonies in winter using a Keller-Segel model with sign-changing chemotactic coefficient
Robbin Bastiaansen, Arjen Doelman, Frank van Langevelde, Vivi Rottschäfer (2020)
[DOI]
Siam Journal on Applied Mathematics 80(2) 839-863
Abstract
Thermoregulation in honey bee colonies during winter is thought to be self-organised. We added mortality of individual honey bees to an existing model of thermoregulation to account for elevated losses of bees that are reported worldwide. The aim of analysis is to obtain a better fundamental understanding of the consequences of individual mortality during winter. This model resembles the well-known Keller-Segel model. In contrast to the often studied Keller-Segel models, our model includes a chemotactic coefficient of which the sign can change as honey bees have a preferred temperature: when the local temperature is too low, they move towards higher temperatures, whereas the opposite is true for too high temperatures. Our study shows that we can distinguish two states of the colony: one in which the colony size is above a certain critical number of bees in which the bees can keep the core temperature of the colony above the threshold temperature, and one in which the core temperature drops below the critical threshold and the mortality of the bees increases dramatically, leading to a sudden death of the colony. This model behaviour may explain the globally observed honey bee colony losses during winter.
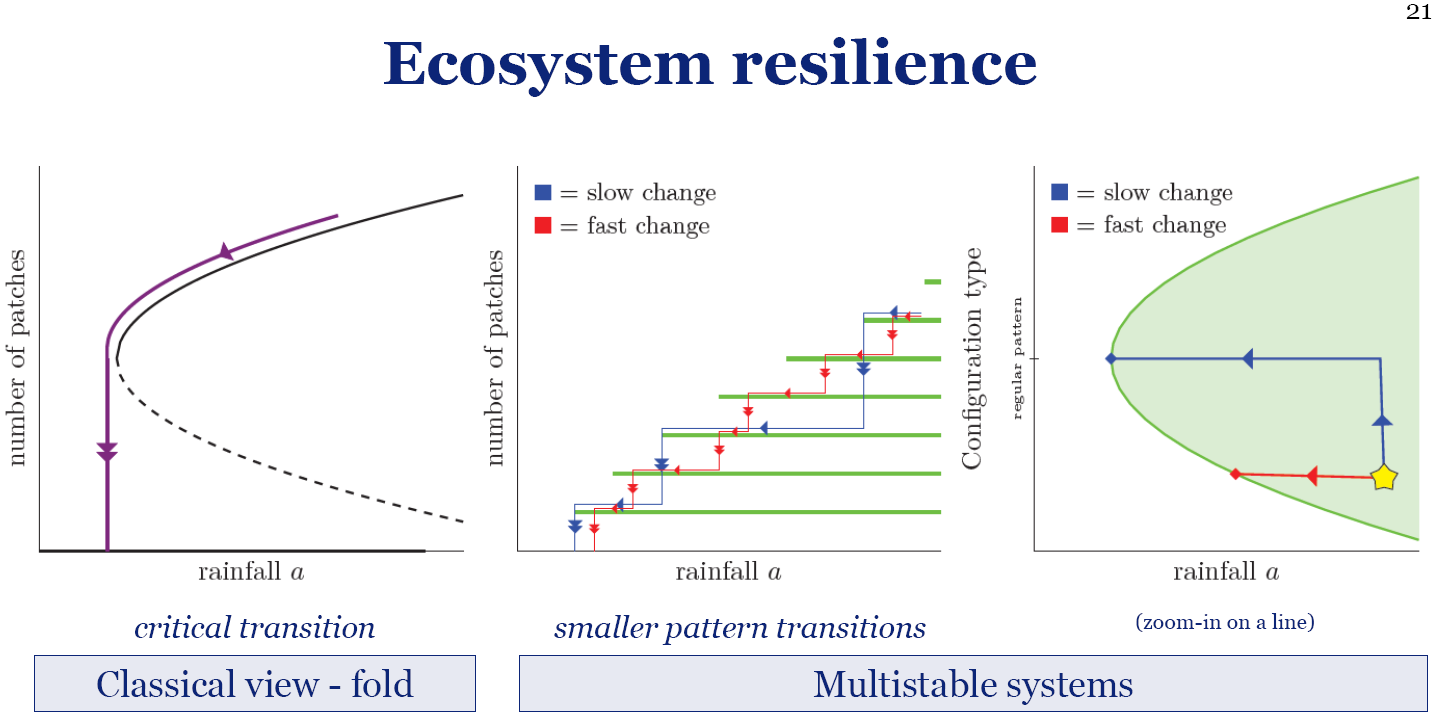
The effect of climate change on the resilience of ecosystems with adaptive spatial pattern formation
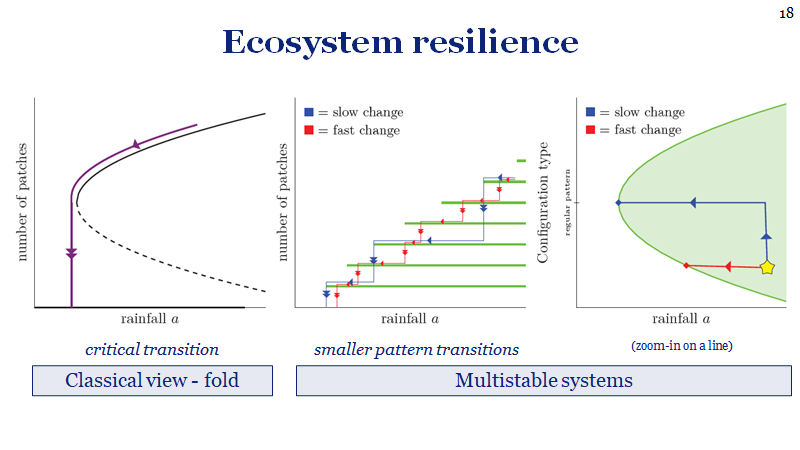
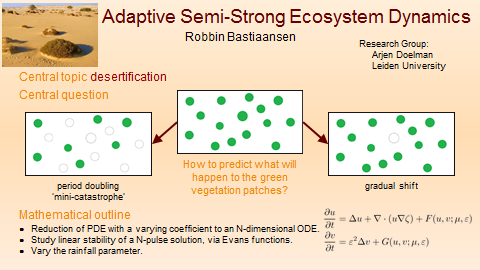
Robbin Bastiaansen, Arjen Doelman, Maarten B. Eppinga, Max Rietkerk (2020)
[DOI]
Ecology Letters 23: 414-429
Abstract
In a rapidly changing world, quantifying ecosystem resilience is an important challenge. Historically, resilience has been defined via models that do not take spatial effects into account. These systems can only adapt via uniform adjustments. In reality, however, the response is not necessarily uniform, and can lead to the formation of (self‐organised) spatial patterns – typically localised vegetation patches. Classical measures of resilience cannot capture the emerging dynamics in spatially self‐organised systems, including transitions between patterned states that have limited impact on ecosystem structure and productivity. We present a framework of interlinked phase portraits that appropriately quantifies the resilience of patterned states, which depends on the number of patches, the distances between them and environmental conditions. We show how classical resilience concepts fail to distinguish between small and large pattern transitions, and find that the variance in interpatch distances provides a suitable indicator for the type of imminent transition. Subsequently, we describe the dependency of ecosystem degradation based on the rate of climatic change: slow change leads to sporadic, large transitions, whereas fast change causes a rapid sequence of smaller transitions. Finally, we discuss how pre-emptive removal of patches can minimise productivity losses during pattern transitions, constituting a viable conservation strategy.
Pulse solutions for an extended Klausmeier model with spatially varying coefficients
Robbin Bastiaansen, Martina Chirilus-Bruckner, Arjen Doelman (2020)
[DOI]
SIAM Journal on Applied Dynamical Systems 19(1) 1-57
Abstract
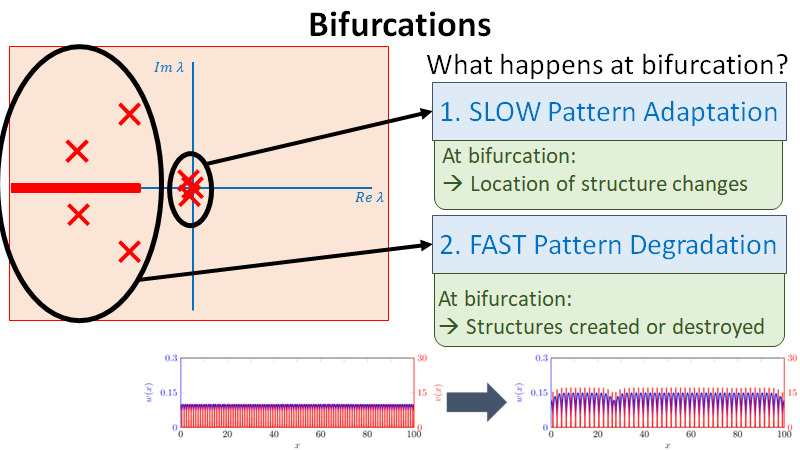
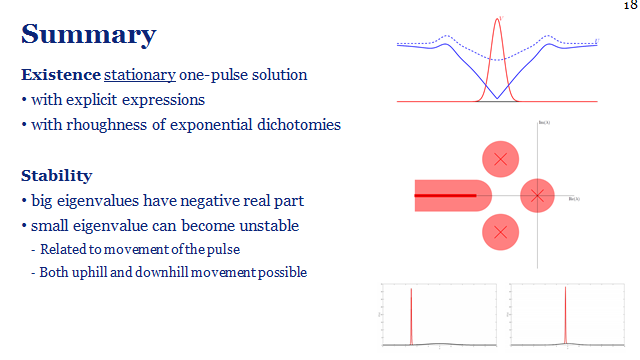
Motivated by its application in ecology, we consider an extended Klausmeier model, a singularly perturbed reaction-advection-diffusion equation with spatially varying coeffcients. We rigorously establish existence of stationary pulse solutions by blending techniques from geometric singular perturbation theory with bounds derived from the theory of exponential dichotomies. Moreover, the spectral stability of these solutions is determined, using similar methods. It is found that, due to the break-down of translation invariance, the presence of spatially varying terms can stabilize or destabilize a pulse solution. In particular, this leads to the discovery of a pitchfork bifurcation and existence of stationary multi-pulse solutions.
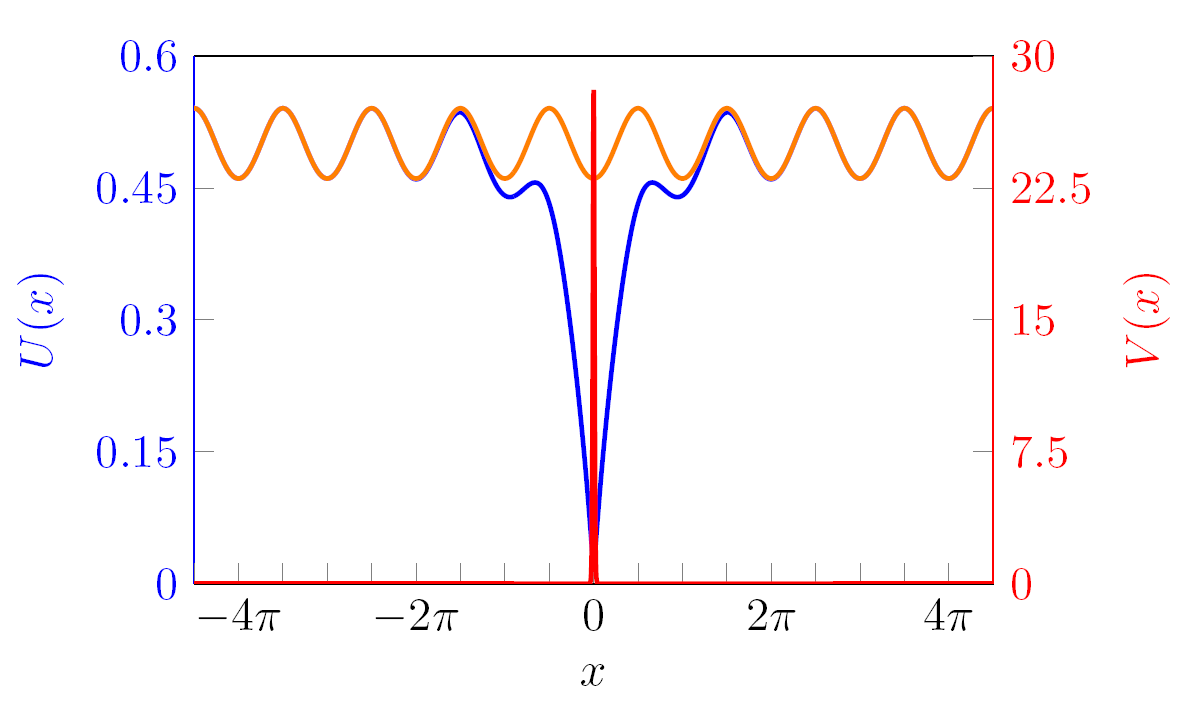
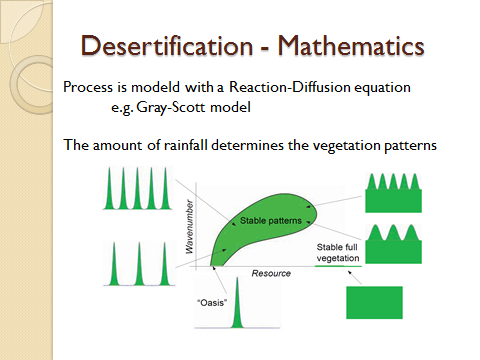
Stable planar vegetation stripe patterns on sloped terrain in dryland ecosystems
Robbin Bastiaansen, Paul Carter, Arjen Doelman (2019)
[DOI]
Nonlinearity 32 2759
Abstract
In water-limited regions, competition for water resources results in the formation of vegetation patterns; on sloped terrain, one finds that the vegetation typically aligns in stripes or arcs. We consider a two-component reaction-diffusion-advection model of Klausmeier type describing the interplay of vegetation and water resources and the resulting dynamics of these patterns. We focus on the large advection limit on constantly sloped terrain, in which the diffusion of water is neglected in favor of advection of water downslope. Planar vegetation pattern solutions are shown to satisfy an associated singularly perturbed traveling wave equation, and we construct a variety of traveling stripe and front solutions using methods of geometric singular perturbation theory. In contrast to prior studies of similar models, we show that the resulting patterns are spectrally stable to perturbations in two spatial dimensions using exponential dichotomies and Lin's method. We also discuss implications for the appearance of curved stripe patterns on slopes in the absence of terrain curvature.
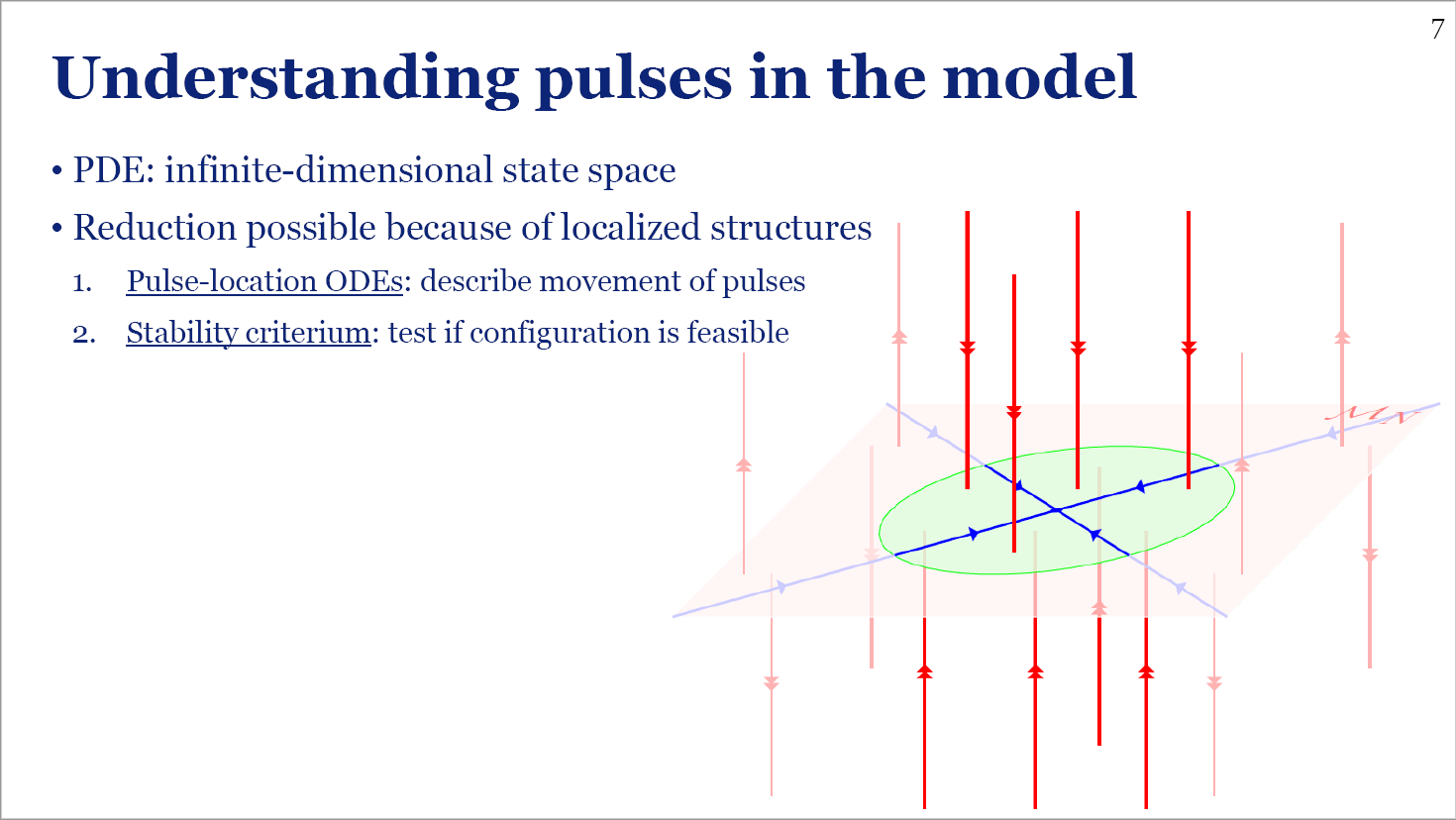
The dynamics of disappearing pulses in a singularly perturbed reaction-diffusion system with parameters that vary in time and space
Robbin Bastiaansen, Arjen Doelman (2019)
[DOI]
Physica D 388: 45-72
Abstract
We consider the evolution of multi-pulse patterns in an extended Klausmeier equation with parameters that change in time and/or space. We formally show that the full PDE dynamics of a \(N\)-pulse configuration can be reduced to a \(N\)-dimensional dynamical system describing the dynamics on a \(N\)-dimensional manifold \(\mathcal{M}_N\). Next, we determine the local stability of \(\mathcal{M}_N\) via the quasi-steady spectrum associated to evolving \(N\)-pulse patterns, which provides provides explicit information on the boundary \(\partial\mathcal{M}_N\). Following the dynamics on \(\mathcal{M}_N\), a \(N\)-pulse pattern may move through \(\partial\mathcal{M}_N\) and 'fall off' \(\mathcal{M}_N\). A direct nonlinear extrapolation of our linear analysis predicts the subsequent fast PDE dynamics as the pattern `jumps' to another invariant manifold \(\mathcal{M}_M\), and specifically predicts the number \(N-M\) of pulses that disappear. Combining the asymptotic analysis with numerical simulations of the dynamics on the various invariant manifolds yields a hybrid asymptotic-numerical method describing the full process that starts with a \(N\)-pulse pattern and typically ends in the trivial homogeneous state without pulses. We extensively test this method against PDE simulations and deduce general conjectures on the nature of pulse interactions with disappearing pulses. We especially consider the differences between the evolution of irregular and regular patterns. In the former case, the disappearing process is gradual: irregular patterns loose their pulses one by one. In contrast, regular, spatially periodic, patterns undergo catastrophic transitions in which either half or all pulses disappear. However, making a precise distinction between these two drastically different processes is quite subtle, since irregular \(N\)-pulse patterns that do not cross \(\partial\mathcal{M}_N\) typically evolve towards regularity.
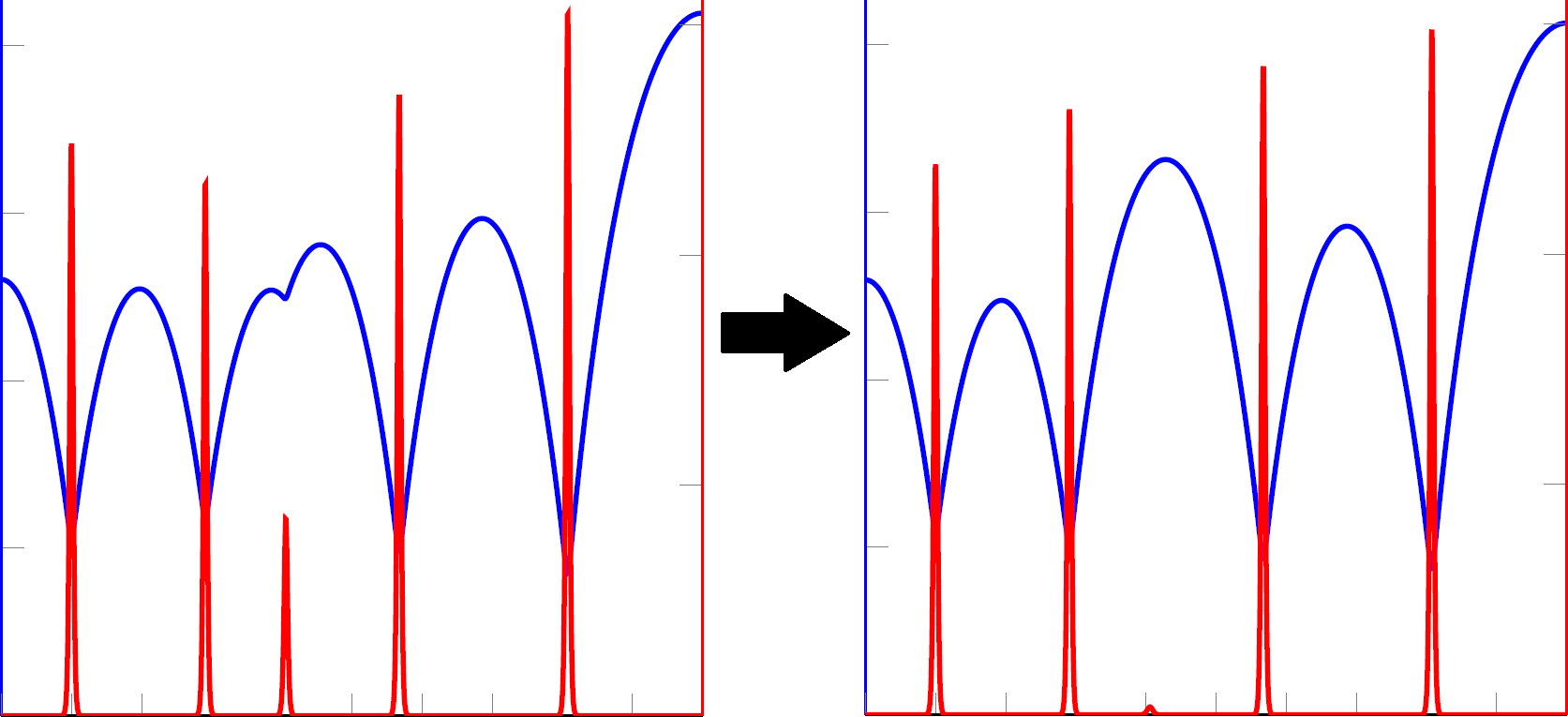
Multi-stability of model and real dryland ecosystems through spatial self-organization
Robbin Bastiaansen, Olfa Jaïbi, Vincent Deblauwe, Maarten Eppinga, Koen Siteur, Eric Siero, Stéphane Mermozh, Alexandre Bouvet, Arjen Doelman, Max Rietkerk (2018)
[DOI]
PNAS 115 (44) 11256-11261
Abstract
Spatial self-organization of dryland vegetation constitutes one of the most promising indicators for an ecosystem’s proximity to desertification. This insight is based on studies of reaction–diffusion models that reproduce visual characteristics of vegetation patterns observed on aerial photographs. However, until now, the development of reliable early warning systems has been hampered by the lack of more in-depth comparisons between model predictions and real ecosystem patterns. In this paper, we combined topographical data, (remotely sensed) optical data, and in situ biomass measurements from two sites in Somalia to generate a multilevel description of dryland vegetation patterns. We performed an in-depth comparison between these observed vegetation pattern characteristics and predictions made by the extended-Klausmeier model for dryland vegetation patterning. Consistent with model predictions, we found that for a given topography, there is multistability of ecosystem states with different pattern wavenumbers. Furthermore, observations corroborated model predictions regarding the relationships between pattern wavenumber, total biomass, and maximum biomass. In contrast, model predictions regarding the role of slope angles were not corroborated by the empirical data, suggesting that inclusion of small-scale topographical heterogeneity is a promising avenue for future model development. Our findings suggest that patterned dryland ecosystems may be more resilient to environmental change than previously anticipated, but this enhanced resilience crucially depends on the adaptive capacity of vegetation patterns.